Cara Menggambar Parabola Fungsi Kuadrat

Dalam fungsi kuadrat ada materi dimana kita harus menggambar Parabola Fungsi Kuadrat atau Grafik Fungsi Kuadrat. Biasa banyak siswa-siswi yang kesulitan untuk menggambar Parabola Fungsi Kuadrat ini atau bahkan mereka sudah malas, karena menurut mereka terlalu sulit. Namun sebanarnya jika kita berfikir secara sistematis akan sangat mudah sekali untuk menggambar Parabola Fungsi Kuadrat dengan sangat mudah. Maksud dari sistematis di sini artinya kalian harus tau langkah-langkah atau urutan-uratan cara untuk membuat Parabola Fungsi Kuadrat atau Grafik Fungsi Kuadrat ini. adapun langkah langkahnya adalah sebagai berikut :

Langkah - Langkah Untuk Menggambar Parabola atau Grafik Fungsi Kuadrat

Bentuk umum fungsi kuadrat adalah : f(x) = ax² + bx + c diamana a, b , c adalah bilangan real dan a tidak sama dengan 0. Grafik fungsi kuadrat berbenruk parabola dengan persamaan y = ax² + bx + c.
Beberapa langkah yang ditempuh untuk menggambar parabola fungsi kuadra, diantaranya :

1. Menentukan titik potong grafik dengan sumbu x, dengan mengambil y = 0
2. Menentukan titik potong grafik dengan sumbu y, dengan mengambil x = 0
3. Menentukan sumbuh simetri grafik yaitu dengan rumus x = -b/2a
4. Menentukan koordinat titik balik atau titik puncak (x,y) dengan rumus x = -b/2a dan y = -D/4a, dengan D = b² - 4ac
5. Menentukan grafiknya terbuka kebawah jika a < 0 atau terbuka ke atas jika a > 0

Contoh Soal Menggambar Parabola Fungsi Kuadrat

Gambarlah parabola dari f(x) = x² - 2x - 8 dengan domain bilangan real !!!!!!

Jawab :

Untuk menggambar parabola kita gunakan langkah - langkah yang sudah saya jelaskan tadi di atas :

1. Menentukan titik potong grafik dengan sumbu x, dengan mengambil y = 0
   x² - 2x - 8 = 0
   Kemudian kita faktorkan menjadi :
   ( x - 4 ) ( x + 2 ) = 0
   Maka akarnya :
   x - 4  = 0
   x - 4 + 4 = 0 + 4
   x = 4
   atau :
   x + 2 = 0
   x + 2 - 2 = 0 - 2
   x = -2
   Maka titik potong dengan sumbu x adalah ( -2, 0 ) ( 4, 0 ).
   Nilai x = 4 dan x = -2 disebut pembuat nol fungsi, artinya pada x = 4 dan x = -2 fungsi tersebut bernilai nol
2. Menentukan titik potong grafik dengan sumbu y, dengan mengambil x = 0
   y = 0² - 2(0) - 8
   y = -8
   Maka titik potong grafik dengan sumbu y adalah ( 0, - 8 ) 
3. Menentukan sumbuh simetri grafik yaitu dengan rumus x = -b/2a
   pada persamaan f(x) = x² - 2x - 8, di dapat :
   a = 1
   b = -2
   c = -8
   maka kita masukan kedalam rumua x = -b/2a, menjadi :
   x = -(-2)/2(1)
   x = 1
   maka sumbu simetri x = 1 
4. Menentukan koordinat titik balik atau titik puncak (x,y) dengan rumus x = -b/2a dan y = -D/4a, dengan D = b² - 4ac
   Karena a = 1, b = -2, dan c = -8, maka :
   x = -b/2a
   x = -(-2)/2(1)
   x = 1
   dan :
   y = -D/4a
   y = -(b² - 4ac)/4a
   y = -(2² - 4(1)(-8))/4(1)
   y = -(4 + 32)/4
   y = -(36)/4
   y = -36/4
   y = -9
   Maka titik balik atau titik puncaknya adalah (1, -9) 
5. Menentukan grafiknya terbuka kebawah jika a < 0 atau terbuka ke atas jika a > 0
   Karena a = 1 dan artinya a > 0 maka grafik atau parabola pasti terbuka ke atas :

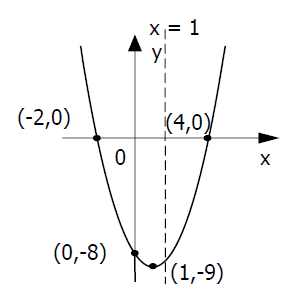Parabola f(x) = x² - 2x - 8

Kesimpulan

Jadi kesimpulannya untuk menggambar parabola atau grafik fungsi kuadrat ada 5 cara diantarnya adalah :

1. Menentukan titik potong grafik dengan sumbu x, dengan mengambil y = 0
2. Menentukan titik potong grafik dengan sumbu y, dengan mengambil x = 0
3. Menentukan sumbuh simetri grafik yaitu dengan rumus x = -b/2a
4. Menentukan koordinat titik balik atau titik puncak (x,y) dengan rumus x = -b/2a dan y = -D/4a, dengan D = b² - 4ac
5. Menentukan grafiknya terbuka kebawah jika a < 0 atau terbuka ke atas jika a > 0

Sumber:
https://matematikaakuntansi.blogspot.com/2016/09/cara-menggambar-parabola-fungsi-kuadrat.html