
Matriks
adalah suatu susunan elemen-elemen atau entri-entri yang berbentuk persegi
panjang yang diatur dalam baris dan kolom. Susunan elemen ini diletakkan dalam
tanda kurung biasa ( ), atau kurung siku [ ]. Elemen-elemen atau entri-entri
tersebut dapat berupa bilangan atau berupa huruf.
Matriks dinotasikan dengan huruf kapital seperti A, B, C dan seterusnya. Sedangkan elemennya jika berupa huruf maka ditulis dengan huruf kecil.
Matriks dinotasikan dengan huruf kapital seperti A, B, C dan seterusnya. Sedangkan elemennya jika berupa huruf maka ditulis dengan huruf kecil.
Dalam
matriks 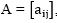 dengan i dan j merupakan bilangan bulat yang menunjukkan baris ke-i dan
kolom ke-j. Misalnya
dengan i dan j merupakan bilangan bulat yang menunjukkan baris ke-i dan
kolom ke-j. Misalnya 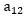 artinya elemen baris ke-1 dan
kolom ke-2.
artinya elemen baris ke-1 dan
kolom ke-2.
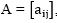 dengan i dan j merupakan bilangan bulat yang menunjukkan baris ke-i dan
kolom ke-j. Misalnya
dengan i dan j merupakan bilangan bulat yang menunjukkan baris ke-i dan
kolom ke-j. Misalnya 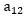 artinya elemen baris ke-1 dan
kolom ke-2.
artinya elemen baris ke-1 dan
kolom ke-2.
Dari matriks A diatas :
a.
Banyaknya baris adalah 4.
b.
Banyaknya kolom adalah 5.
c.
Elemen-elemen baris ke-3 adalah 0, 5, 1,7, -1.
d.
Elemen-elemen baris ke-4 adalah 9, 2, 6, 1, 0.
e.
Elemen-elemen kolom ke-1 adalah -1, 4, 0, 9.
f.
Elemen-elemen kolom ke-4 adalah 7, -3, 7, 1.
g.
Elemen baris ke-2 dan kolom ke-3 atau 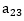 adalah 9.
adalah 9.
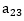 adalah 9.
adalah 9.
h.
Elemen baris ke-3 dan kolom ke-5 atau 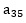 adalah -1.
adalah -1.
B. Ordo Matriks
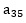 adalah -1.
adalah -1. B. Ordo Matriks
Ordo
(ukuran) dari matriks adalah banyaknya elemen baris diikuti banyaknya kolom.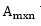 berarti matriks A berordo m x n,
artinya matriks tersebut mempunyai m buah baris dan n buah kolom.
berarti matriks A berordo m x n,
artinya matriks tersebut mempunyai m buah baris dan n buah kolom.
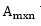 berarti matriks A berordo m x n,
artinya matriks tersebut mempunyai m buah baris dan n buah kolom.
berarti matriks A berordo m x n,
artinya matriks tersebut mempunyai m buah baris dan n buah kolom.
Contoh :
Tentukan ordo dari
matriks dibawah ini !
a. 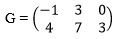 b.
b.
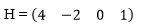
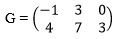 b.
b.
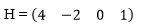
Jawab :
a.
Matriks G terdiri dari 2 baris dan 3 kolom, maka matriks G berordo 2 x 3,
atau ditulis G2X3.
b.
Matriks H terdiri dari 1 baris dan 4 kolom, maka matriks H berordo 1 x 4,
atau ditulis H1X4.
C. Jenis - Jenis Matriks
C. Jenis - Jenis Matriks
1.
Matriks Nol
Matriks nol adalah matriks yang seluruh elemennya
nol.
2.
Matriks Kolom
Matriks kolom adalah matriks yang hanya terdiri dari
satu kolom.
3.
Matriks Baris
Matriks baris adalah matriks yang hanya terdiri dari
satu baris
4.
Matriks Persegi atau Bujur Sangkar
Matriks persegi adalah matriks yang banyaknya baris
sama dengan banyaknya kolom.
5.
Matriks Diagonal
Matriks diagonal adalah matriks yang seluruh
elemennya nol kecuali pada diagonal utamanya tidak semuanya nol.
6.
Matriks Segitiga
Matriks segitiga terdiri atas dua macam yaitu
matriks segitiga atas dan matriks segitiga bawah.
Matriks segitiga atas adalah matriks yang
elemen-elemen dibawah diagonal utama seluruhnya nol.
Matriks
segitiga bawah adalah matriks yang elemen-elemen diatas diagonal utama
seluruhnya nol.
7.
Matriks Identitas
Matriks identitas adalah matriks yang semua elemen
pada diagonal utamanya adalah satu dan elemen lainnya adalah nol.
Contoh :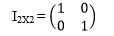
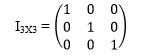
D. Transpose Matriks
Contoh :
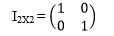
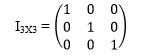
D. Transpose Matriks
Transpose matriks A = (aij) dengan ordo m
x n ditulis AT = (aij) dan mempunyai ordo n x m.
Elemen-elemen baris matriks AT diperoleh dari elemen-elemen kolom
matriks A dan sebaliknya.
Dua matriks dikatakan sama, apabila mempunyai ordo
sama dan elemen-elemen yang seletak (bersesuaian) dari kedua matriks tersebut
sama.
Matriks A = B karena ordo dan elemen-elemen yang
seletak dari kedua matriks tersebut sama. Sedangkan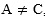 walaupun elemennya sama tetapi tidak
seletak.
walaupun elemennya sama tetapi tidak
seletak.
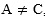 walaupun elemennya sama tetapi tidak
seletak.
walaupun elemennya sama tetapi tidak
seletak.
Contoh :
Jawab :
·
Elemen baris 1 kolom 1 (a11) : 2x = 4
x = 2
·
Elemen baris 1 kolom 3 (a13) : 2 + x = y
y = 2 +
2 = 4
·
Elemen baris 2 kolom 1 (a21) : z = 3y
z = 3.4
= 12
·
Elemen baris 2 kolom 2 (a22) : a + 1 = 4z
a + 1 = 4.12
a = 48 – 1 = 47
·
Elemen baris 3 kolom 1 (a31) : b = a + 5
b = 47 + 5
b = 52
F. Operasi Matriks
- Penjumlahan dan Pengurangan Matriks
Dua matriks A dan B dapat dijumlahkan atau digunakan
operasi pengurangan bila ordo (baris x kolom) kedua matriks tersebut sama.
Hasil jumlah (selisih) didapat dengan cara menjumlahkan (mengurangkan)
elemen-elemen yang seletak dari kedua matriks tersebut.
A + C tidak dapat
dijumlahkan, ordo kedua matriks tersebut tidak sama.
Sifat-sifat operasi
penjumlahan dan pengurangan pada matriks
Untuk setiap matriks A,
B dan C yang berordo sama, berlaku :
a.
A + (B + C) = (A + B) + C sifat assosiatif.
b.
A + B = B + A sifat komutatif.
c.
A(B + C) = AB + AC sifat distributif.
d.
A(B – C) = AB – AC.
e.
A + 0 = 0 + A = A.
f.
Terdapat matriks X sedemikian sehingga A + X = B.
- Perkalian Matriks
1. Perkalian Matriks dengan Skalar (K)
Misalkan k
sebuah skalar dan A sebuah matriks maka kA adalah sebuah matriks yang didapat
dengan cara mengalikan setiap elemen (entri) matriks A dengan skalar k.
Sifat-sifat perkalian
matriks dengan skalar.
Untuk setiap skalar k1
dan k2 dan untuk setiap matriks A dan B yang berordo sama dan
AB terdefinisi, maka berlaku :
a.
(k1 + k2) A = k1 A + k2 A.
b.
(k1 – k2) A = k1 A – k2 A.
c.
(k1 k2) A = k1 (k2 A).
d.
k1 (A B) = (k1 A) B.
e.
k1 (A + B) = k1 A + k1 B.
f.
k1 (A – B) = k1 A
- k1 B.
2.
Perkalian Matriks dengan Matriks
Dua matriks
A dengan ordo m x n dan matriks B dengan ordo n x p, hasil kali antara A dan B
adalah sebuah matriks C = A . B yang berordo m x p, didapat dengan cara
mengalikan setiap elemen baris matriks A dengan elemen kolom matriks B.
Contoh :

diperoleh dengan cara mengalikan elemen-elemen baris ke-1 matriks sebelah kiri (matriks A) dengan elemen-elemen kolom ke-2 matriks sebelah kanan (matriks B) kemudian menjumlahkannya. Demikian seterusnya untuk mengisi kotak-kotak tersebut.

diperoleh dengan cara mengalikan elemen-elemen baris ke-1 matriks sebelah kiri (matriks A) dengan elemen-elemen kolom ke-2 matriks sebelah kanan (matriks B) kemudian menjumlahkannya. Demikian seterusnya untuk mengisi kotak-kotak tersebut.
Contoh :
(sebelah kiri) dengan banyaknya baris matriks kedua (sebelah kanan) tidak sama.
Contoh :
G. Determinan Matriks
1. Determinan Matriks Ordo 2
Contoh :
Contoh :
2. Determinan Matriks Ordo 3
Misalkan matriks persegi dengan ordo tiga, diberikan dibawah ini
 , determinan dari matriks A adalah Det (A) =
, determinan dari matriks A adalah Det (A) = . Banyak cara yang dapat digunakan untuk menghitung determinan matriks
dengan ordo 3x3, tetapi yang paling banyak digunakan adalah dengan menggunakan
aturan Sarrus. Dengan langkah-langkah sebagai berikut :
. Banyak cara yang dapat digunakan untuk menghitung determinan matriks
dengan ordo 3x3, tetapi yang paling banyak digunakan adalah dengan menggunakan
aturan Sarrus. Dengan langkah-langkah sebagai berikut :
 , determinan dari matriks A adalah Det (A) =
, determinan dari matriks A adalah Det (A) = . Banyak cara yang dapat digunakan untuk menghitung determinan matriks
dengan ordo 3x3, tetapi yang paling banyak digunakan adalah dengan menggunakan
aturan Sarrus. Dengan langkah-langkah sebagai berikut :
. Banyak cara yang dapat digunakan untuk menghitung determinan matriks
dengan ordo 3x3, tetapi yang paling banyak digunakan adalah dengan menggunakan
aturan Sarrus. Dengan langkah-langkah sebagai berikut :
·
Letakkan kolom pertama dan kedua disebelah kanan garis vertikal dari
determinan.
·
Jumlahkan hasil kali unsur-unsur yang terletak pada diagonal utama dengan
hasil kali unsur-unsur sejajar diagonal utama pada arah kanan, kemudian
dikurangi dengan hasil kali unsur-unsur yang terletak sejajar dengan diagonal
samping.
Perhatikan skema untuk
menghitung dengan menggunakan sarrus dibawah ini !
= (a11)(a22)(a33) + (a12)(a23)(a31) + (a13)(a21)(a32) – (a31)(a22)(a13) – (a32)(a23)(a11) – (a32)(a21)(a12)
= (a11)(a22)(a33) + (a12)(a23)(a31) + (a13)(a21)(a32) – (a31)(a22)(a13) – (a32)(a23)(a11) – (a32)(a21)(a12)
Contoh :
= 1.3.3 +
2.4.1 + 3.1.4 – 1.3.3 – 4.4.1 – 3.1.2
= 9 + 8 + 12
– 9 – 16 – 6
= 29 – 31 =
-2
Contoh :
Jawab :
Det (A) = (x – 1).2.5 + 1.(-4).3x + 3.(-1).2 – 3x.2.3 – 2.(-4).(x-1) -
5.(-1).1
= (x – 1).10 – 12x – 6 – 18x + 8(x – 1) + 5
= 10x – 10 - 12x – 6 – 18x + 8x – 8 + 5
= -12x – 19
Det (A) = 6
-12x – 19 = 6
Jika A
adalah sebuah matriks persegi, maka minor entri atau elemen aij
dinyatakan oleh Mij dan didefinisikan sebagai determinan sub matriks
yang tinggal setelah baris ke-i dan kolom ke-j dicoret dari A. Bilangan (-1)i+j
Mij dinyatakan oleh Cij
dinamakan kofaktor entri aij.
Disebut
matriks kofaktor dari A. Transpose matriks ini disebut adjoin dari A dan
dinyatakan dengan Adj (A).
Contoh :
Jawab :
Minor dari matriks A
adalah :
Kofaktor dari matriks A
adalah :
C11
= (-1)1+1 M11 = (1) 6 = 6 C21
= (-1)2+1 M21 = (-1) 3 = -3
C12 =
(-1)1+2 M12 = (-1) 2 = -2 C22
=(-1)2+2 M22 = (1)(-1) =-1
Adjoin dari matriks
kofaktor adalah transpose dari matriks kofaktor, sehingga :
Contoh :
Kofaktor dari minor-minor tersebut adalah :
C11
= (-1)1+1 M11 = (1)(11) = 11 C23 =(-1)2+3 M23
=-1.(-26)=26
C12
= (-1)1+2 M12 = (-1)(8) = -8 C31 = (-1)3+1 M31 =
(1)(8) = -8
C13
= (-1)1+3 M13 = (1)(3) = 3 C32 = (-1)3+2 M32
=-1.(-4) = 4
C21
= (-1)2+1 M21 = (-1)(-42) = 42 C33 = (-1)3+3 M33 = 1(-4)
= -4
C22
= (-1)2+2 M22 = (1)(-36) = -3
Matriks Kofaktor adalah
:

Adjoin dari matriks
kofaktor adalah transpose dari Matriks kofaktor, sehingga :


I. Invers Matriks
Jika A dan B
adalah matriks persegi yang berordo sama sedemikian sehingga hasil kali AB = BA
= I, dengan I matriks identitas maka B adalah invers dari A dan sebaliknya,
yaitu B = A-I atau A = B-I.
Contoh :
Diketahui . Tunjukkan bahwa kedua matriks tersebut adalah saling invers.
. Tunjukkan bahwa kedua matriks tersebut adalah saling invers.
 . Tunjukkan bahwa kedua matriks tersebut adalah saling invers.
. Tunjukkan bahwa kedua matriks tersebut adalah saling invers.Karena AB = BA = I, maka B = A-I dan A = B-I.
Contoh :
Jawab :
Determinan A (det(A))
adalah det .
.
Minor dari A adalah :
 .
. Minor dari A adalah :
Kofaktor dari A adalah :
C11
= (-1)1+1 M11 = d C21
= (-1)2+1 M21 = -b
C12 =
(-1)1+2 M12 = -c C22
= (-1)2+2 M22 = a
Matriks Kofaktor sedangkan matriks adjoin :
sedangkan matriks adjoin :
 sedangkan matriks adjoin :
sedangkan matriks adjoin :Sehingga invers matriks A adalah :
Contoh :
Dengan menggunakan hasil
terakhir pada contoh diatas, tentukanlah invers dari :
a. Det (A) = 4.1 – 3.2 = -2 sehingga:
b. Det (A) = (-2.1.3 + 2.-1.5 + 8.1.8) – (6.1.5 + -2.-1.8 + 3.1.2)
= (-6 – 10 + 64) – (30 + 16 + 6) = -4
Catatan :
·
Matriks yang mempunyai invers adalah matriks yang nilai determinannya  0, matriks seperti ini disebut Matriks Non
Singular. Sedangkan
matriks yang harga determinannya = 0 disebut Matriks Singular.
0, matriks seperti ini disebut Matriks Non
Singular. Sedangkan
matriks yang harga determinannya = 0 disebut Matriks Singular.
 0, matriks seperti ini disebut Matriks Non
Singular. Sedangkan
matriks yang harga determinannya = 0 disebut Matriks Singular.
0, matriks seperti ini disebut Matriks Non
Singular. Sedangkan
matriks yang harga determinannya = 0 disebut Matriks Singular.
·
Invers suatu matriks jika ada adalah tunggal dan berlaku sifat :
§
(A-I )-I = A
§
(A x B)-I = B-I
x A-I
Contoh :
Contoh :
Jawab :
a.
Det (A) = 2.6 – 3.4 = 12 – 12 = 0, karena determinannya 0 maka disebut
matriks singular.
b.
Det (B) = 4.(-5) – (-2).(-10) = -20 – 20 = -40, Karena determinannya
tidak 0 maka disebut matriks non singular.
Contoh :
Ternyata dari jawaban a dan b contoh soal diatas, diperoleh kesimpulan (A
x B)-I = B-I x A-I.
J. Menyelesaikan
Sistem Persamaan Linear
Sistem
persamaan linear dua atau tiga variabel selain dengan menggunakan eliminasi dan
substitusi dapat juga digunakan invers dan kaidah Creamer untuk mencari
himpunan penyelesaiannya.
Beberapa
langkah yang perlu diperhatikan untuk mencari himpunan penyelesaian sistem
persamaan linear dengan menggunakan invers, adalah :
·
Tulislah sistem persamaan dalam bentuk matriks.
· Kalikan kedua ruas dengan invers A atau A-I, Sehingga menjadi :
A-I A X = A-I
C
I X = A-I C
X = A-I C
Untuk
persamaan yang berbentuk XA = C, maka untuk mendapatkan X kalikan kedua ruas
dengan A-I dari sebelah kanan, sehingga dapat :
XA A-I = C A-I
X I = C A-I
X = C A-I
Contoh
:
Tentukan
nilai x dan y dari sistem persamaan :
5x + 3y = 4
3x + 2y = 3
Jawab
:
Jadi himpunan penyelesaian dari sistem persamaan tersebut adalah
 . Disamping menggunakan cara invers dapat pula
penyelesaian sistem persamaan linear dicari dengan menggunakan Kaidah Creamer .
. Disamping menggunakan cara invers dapat pula
penyelesaian sistem persamaan linear dicari dengan menggunakan Kaidah Creamer .
Jika AX = C adalah sistem persamaan linear yang terdiri dari n
persamaan linear dan n variabel yang tidak diketahui sehingga det , maka
sistem tersebut mempunyai penyelesaian yang unik (tunggal). Penyelesaian
tersebut adalah
, maka
sistem tersebut mempunyai penyelesaian yang unik (tunggal). Penyelesaian
tersebut adalah dimana
Aj adalah matriks yang didapat dengan cara mengganti entri-entri
didalam koloMke-j dari A dengan entri-entri didalam matriks.
dimana
Aj adalah matriks yang didapat dengan cara mengganti entri-entri
didalam koloMke-j dari A dengan entri-entri didalam matriks.
 , maka
sistem tersebut mempunyai penyelesaian yang unik (tunggal). Penyelesaian
tersebut adalah
, maka
sistem tersebut mempunyai penyelesaian yang unik (tunggal). Penyelesaian
tersebut adalah dimana
Aj adalah matriks yang didapat dengan cara mengganti entri-entri
didalam koloMke-j dari A dengan entri-entri didalam matriks.
dimana
Aj adalah matriks yang didapat dengan cara mengganti entri-entri
didalam koloMke-j dari A dengan entri-entri didalam matriks.
Contoh
:
Gunakan
kaidah Creamer untuk mencari himpunan penyelesaian sistem berikut ini!
3x – 4y = -5
2x + y = 4
Jadi
himpunan penyelesaian dari sistem persamaan adalah {(1,2)}.
Contoh
:
Tentukan
penyelesaian dari sistem persamaan dengan menggunakan Kaidah Creamer !
x + 2z = 7
-3x + 4y + 6z = 7
-x – 2y + 3z = 12
Jawab
:
Jawab :
Sumber: Klik DISINI
































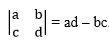 .
.































Tidak ada komentar:
Posting Komentar