Matriks 2 (Invers & Adjoin 2 x 2)

INVERS MATRIKS:

Jika A dan B adalah matriks persegi, dan berlaku  maka dikatakan matriks A dan B saling invers. B disebut invers dari A, atau ditulis 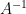. Matriks yang mempunyai invers disebut invertible atau matriks non singular, sedangkan matriks yang tidak mempunyai invers disebut matriks singular.

Untuk mencari invers matriks persegi berordo 2×2, coba perhatikan berikut ini.
Jika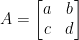  dengan , maka invers dari matriks A (ditulis 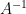) adalah sebagai berikut:

Jika  maka matriks tersebut tidak mempunyai invers, atau disebut matriks singular.

Sifat-sifat matriks persegi yang mempunyai invers:

• 
• 
• 

Contoh: Diketahui A =  dan B = 

Selidiki, apakah A dan B saling invers?

Penyelesaian :

Matriks A dan B saling invers jika berlaku A × B = B × A = I.

A × B = 

B × A = 

Karena A × B = B × A maka A dan B saling invers, dengan A^–1 = B dan B^–1 = A.

Menentukan Invers Matriks Berordo 2 × 2

Misalkan diketahui matriks A =  , dengan ad – bc ≠ 0.

Suatu matriks lain, misalnya B dikatakan sebagai invers matriks A jika AB = I. Matriks invers dari A ditulis A^–1 . Dengan demikian, berlaku :

AA^–1 = A^–1A = I

Matriks A mempunyai invers jika A adalah matriks nonsingular, yaitu det A ≠ 0. Sebaliknya, jika A matriks singular (det A = 0) maka matriks ini tidak memiliki invers.

Misalkan matriks A =  dan matriks B =  sehingga berlaku A × B = B × A = I. Kita akan mencari elemen-elemen matriks B, yaitu p, q, r, dan s.

Dari persamaan A × B = I, diperoleh :

Jadi, diperoleh sistem persamaan :

ap + br = 1  dan  aq + bs = 0

cp + dr = 0         cq + ds = 1

Dengan menyelesaikan sistem persamaan tersebut, kalian peroleh :

Dengan demikian,

Matriks B memenuhi A × B = I.

Sekarang, akan kita buktikan apakah matriks B × A = I?

Karena ad – bc ≠ 0, berlaku B × A =  = I

Karena A × B = B × A = I maka B = A^–1.

Jadi, jika A =  maka inversnya adalah :

untuk ad – bc ≠ 0.

Contoh Soal 18 :

Tentukan invers matriks-matriks berikut.

a. A = 

b. B = 

Jawaban: