Contoh Uji Multikolinearitas

...............

Sister Ristekdikti

Uji Reliabilitas

..............

Uji Validitas

.....................

Uji Normalitas

.........................

Uji Heteroskedastisitas

................

Teori Uji Multikolinearitas

Uji multikolinearitas digunakan untuk mengetahui ada atau tidaknya penyimpangan asumsi klasik. Multikolinearitas yaitu adanya hubungan linear antar variabel independen dalam model regresi linier berganda. Prasyarat yang harus terpenuhi dalam model regresi linier berganda adalah tidak adanya multikolinearitas.

Ada beberapa metode pengujian yang bisa digunakan diantaranya yaitu: 1) dengan melihat nilai inflation factor (VIF) pada model regresi linier berganda, 2) dengan membandingkan nilai koefisien determinasi individual (r²) dengan nilai determinasi secara serentak (R²), dan 3) dengan melihat nilai eigenvalue dan condition index. Pada pembahasan ini akan dilakukan uji multikolinearitas dengan melihat nilai inflation factor (VIF) pada model regresi dan membandingkan nilai koefisien determinasi individual (r²) dengan nilai determinasi secara serentak (R²).

Uji Autokorelasi

Persamaan Regresi Linier Berganda (Contoh Kasus Manual) (03)

1. Arti Dari Konstanta, Koefisien X₁ dan
    Koefisien X₂ Dalam Persamaan Regresi
    Linier Berganda.

Persamaan Regresi Linier Berganda di atas dapat dijelaskan sebagai berikut:

- Konstanta sebesar 2,553; artinya jika Harga Barang X (X₁) dan Harga Barang Y (X₂) nilainya adalah 0, maka Jumlah Barang X yang dibeli (Y’) nilainya adalah 2,553 unit.

Contoh Soal Dan Pembahasan Tentang Differensial (01)

SOAL & JAWABAN

Diferensial Fungsi Sederhana

Contoh Soal Dan Pembahasan Tentang Differensial (02)

 

1.    Diketahui , nilai dari f’(5) adalah ...
a.    6
b.    10
c.    14
d.    17
e.    20

PEMBAHASAN:

    f’(x) = 2x + 4
    f’(5) = 2(5) + 4
            = 14

JAWABAN: C

Persamaan Regresi Linier Berganda (Contoh Kasus Manual) (02)

Langkah 9:

Uji Koefisien Regresi Secara Simultan/Bersama-sama (Uji F) !!!

Uji ini digunakan untuk mengetahui apakah variabel independen (X₁,X₂….X_n) secara bersama-sama berpengaruh secara signifikan terhadap variabel dependen (Y). Atau untuk mengetahui apakah model regresi dapat digunakan untuk memprediksi variabel dependen atau tidak. Signifikan berarti hubungan yang terjadi dapat berlaku untuk populasi (dapat digeneralisasikan), misalnya dari kasus di atas sampelnya adalah 10.

Dari hasil perhitungan manual analisis regresi berganda dapat diketahui nilai F seperti pada langkah 7 sebesar 24,57.

Persamaan Regresi Linier Berganda (Contoh Kasus Manual) (01)

Pengolahan Data Regresi Linier Berganda Secara Manual !!!

Langkah 1:

Siapkan DATA MENTAH Y, X1, X2 !!!

Determinan Dengan Metode Cramer

Metode Cramer

jika Ax = b adalah sebuah sistem linear n yang tidak di ketahui dan det(A)≠ 0 maka persamaan tersebut mempunyai penyelesaian yang unik
dimana A _j adalah matrik yang didapat dengan mengganti kolom _j dengan matrik b
Contoh soal:
Gunakan metode cramer untuk menyelesaikan persoalan di bawah ini

x₁ + x₃ = 6

-3x₁ + 4x₂ + 6x₃ = 30

-x₁ - 2x₂ + 3x₃ = 8

Jawab:
Bentuk matrik A dan b

A = b =

Kemudian ganti kolom _j dengan matrik b

A₁ = A₂ = A₃ =

Dengan metode sarrus kita dapat dengan mudah mencari determinan dari matrik-matrik di atas
maka,

Uji Autokorelasi

Teori Uji Autokorelasi !!! Silahkan Buka DISINI
Materi PDF !!! Silahkan DOWNLOAD DISINI

Uji Heteroskedastisitas

Dalam kaitannya dengan kehidupan kita sehari-hari khususnya dalam bidang ekonomi, terkadang kita ingin mengetahui bagaimana hubungan, faktor-faktor, gangguan atau hambatan serta pengaruh apa saja yang terjadi dalam proses dalam kegiatan ekonomi yang kita lakukan. Misalnya, antara biaya produksi dan pendapatan yang diperoleh, antara jumlah tenaga kerja dan jumlah produk yang dihasilkan, antara pola konsumsi orang miskin dan orang kaya, dan sebagainya.

Sebagai contoh, kegiatan yang sering kita jumpai dalam kegiatan sehari-hari adalah adanya perbedaan pola konsumsi antara orang miskin dan orang kaya. Kegiatan yang bisa kita lihat disini adalah orang yang kaya tentu akan bervariasi dalam membelanjakan uangnya. Sedangkan orang yang miskin hanya bisa sedikit bervariasi dalam berbelanja. Hal inilah yang bisa dikatakan adanya varians yang tidak sama antara kedua golongan tersebut, yang berarti timbul masalah heteroskedastisitas.

Persamaan Regresi Linier Berganda

Analisis regresi linier berganda adalah hubungan secara linear antara dua atau lebih variabel independen (X₁, X₂,….X_n) dengan variabel dependen (Y). Analisis ini untuk mengetahui arah hubungan antara variabel independen dengan variabel dependen apakah masing-masing variabel independen berhubungan positif atau negatif dan untuk memprediksi nilai dari variabel dependen apabila nilai variabel independen mengalami kenaikan atau penurunan. Data yang digunakan biasanya berskala interval atau rasio.

Determinan Matriks Metode Sarrus dan Metode Ekspansi Laplace/Ekspansi Kofaktor

Ada dua macam cara menghitung matriks ordo 3×3. Satu yang paling terkenal adalah metode Sarrus dan satunya lagi adalah metode Ekspansi Laplace. Metode kedua ini jarang diketahui mahasiswa. Oleh karena itu saya akan membahasnya disini.

Determinan Matriks Ordo 3 x 3

Apa itu determinan matriks ??

Determinan matriks merupkan salah satu persyatan yang harus dipenuhi dalalm mencari invers suatu matriks. Dalam matriks, cara mencari determinan berbeda untuk setiap ordonya. Kali ini saya akan membahas mengenai cara menentukan determinan matriks ordo 3x3.

Untuk menentukan determinan matriks ordo 3x3 berbeda dengan cara menentukan determinan matriks ordo 2x2, untuk menentukannya yaitu pertama harus menambahkan kolom satu dan kolom dua secara berurutan ke sebelah kiri matriks. Untuk lebih jelasnya perhatikan uraian dibawah ini :

Keterangan :

DM : Determinan Matriks
Ordo : Jenis matriks
a, b, c, d, e, f, g, h, dan i : Elemen-elemen matriks

Invers Matriks 3 x 3

 ................................................

Adjoin Matriks Ordo 3 x 3

Untuk menentukan adjoin sangat-sangat lah mudah. Adjoin merupakan hasil transpose dari kofaktor matriks. Transpose itu adalah mengubah baris menjadi kolom atau sebaliknya. Maka adjoin matriks adalah mengubah baris menjadi kolom atau sebaliknya dari kofaktor matriks. Namun sebelum kita praktek, teman-taman wajib membaca dulu artikel cara menentukan kofaktor matriks pada link di bawah ini :

Cara Menentukan Kofaktor Matriks Ordo 3x3

Adjoin ditentukan dengan mentransposekan kofaktor dari matriks, misalnya kofaktor matriks :

Kofaktor Matriks Ordo 3 x 3

Apa itu kofaktor ???

Secara definisi kofaktor memang sulit untuk dijelaskan. Akan tetapi menurut dari apa yang telah saya pelajari bahwa kofaktor itu adalah salah satu tahapan dalam proses pencarian nilai invers dari suatu matriks.

Minor Matriks Ordo 3 x 3

Sebelum kita bahas tentang cara mencari minor matriks ordo 3x3 , alangkah lebih baiknya teman-teman simak dulu penjelasan tentang matriks dan elemen matriks berikut ini:

Matriks

Matriks adalah sekumpulan bilangan yang disusun secara baris dan kolom dan ditempatkan pada kurung biasa atau kurung siku.

Elemen Matriks

Kata elemen berasal dari kata Latin elementum yang berarti bagian-bagian dasar yang mendasari sesuatu.

Maka elemen matriks adalah bagian-bagian dasar yang mendasari sekumpulan bilangan yang disusun secara baris dan kolom dan ditempatkan pada kurung biasa atau kurung siku.

Nah sekarang apa itu minor matriks ???

Perkalian Matriks 3 x 3

Perkalian matriks 3 x 3 sedikit lebih rumit dari perkalian matriks 2 x 2. Hal ini dikarenakan ukuran matriks 3 x 3 mempunyai jumlah anggota lebih banyak. Matriks persegi dengan ukuran 3 x 3 memiliki 9 anggota, yang terbagi dalam 3 baris dan 3 kolom. Pada matriks dengan ukuran 3 x 3, setiap baris dan kolom terdiri atas 3 anggota. Konsep perkalian pada matriks dengan ukuran 3 x 3 sama dengan proses perkalian matriks dengan ukuran 2 x 2, hanya saja lebih rumit.

Matriks 2 (Invers & Adjoin 2 x 2)

INVERS MATRIKS:

Jika A dan B adalah matriks persegi, dan berlaku  maka dikatakan matriks A dan B saling invers. B disebut invers dari A, atau ditulis 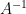. Matriks yang mempunyai invers disebut invertible atau matriks non singular, sedangkan matriks yang tidak mempunyai invers disebut matriks singular.

Untuk mencari invers matriks persegi berordo 2×2, coba perhatikan berikut ini.
Jika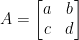  dengan , maka invers dari matriks A (ditulis 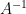) adalah sebagai berikut:

Jika  maka matriks tersebut tidak mempunyai invers, atau disebut matriks singular.

Matriks 2 (Kofaktor 2 x 2)

Kofaktor suatu matriks dirumuskan sebagai (-1) pangkat baris ditambah kolom elemen minor dari matriks bersangkutan. Secara matematis dirumuskan sebagai:

Keterangan:

Matriks 2 (Minor 2 x 2)